Rectangle d'or:
Els rectangles d'or són aquells rectangles els costats dels quals guarden raó àuria.
 La construcció d'un rectangle d'or amb compàs es pot fer molt fàcilment a partir d'un quadrat mitjançant la segona construcció de l'apartat corresponent. Punxant al centre d'un dels costats i obrint fins a un dels dos angles oposats, només cal baixar l'arc fins a la prolongació del costat on s'ha punxat. Una de les propietats dels rectangles d'or és que el rectangle resultant de l'eliminació del quadrat de costat b que el pot generar , també és d'or.
La construcció d'un rectangle d'or amb compàs es pot fer molt fàcilment a partir d'un quadrat mitjançant la segona construcció de l'apartat corresponent. Punxant al centre d'un dels costats i obrint fins a un dels dos angles oposats, només cal baixar l'arc fins a la prolongació del costat on s'ha punxat. Una de les propietats dels rectangles d'or és que el rectangle resultant de l'eliminació del quadrat de costat b que el pot generar , també és d'or. Triangle d'or:
Els triangles d'or són aquells triangles isòsceles els costats dels quals estan en raó àuria. N'hi ha de dos tipus: els que
 , que són acutangles i els que
, que són acutangles i els que  , que són obtusangles. Aquests últims sovint són també anomenats triangles d'argent, però no tenen res a veure amb el nombre d'argent.
, que són obtusangles. Aquests últims sovint són també anomenats triangles d'argent, però no tenen res a veure amb el nombre d'argent.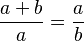


No hay comentarios:
Publicar un comentario